---

1 2

Formas de definir la posición y sus cambios

e puede definir la posición de un cuerpo móvil de tres maneras distintas, dependiendo de si contamos o no con algún dato conocido. Estos métodos pueden ser: escalarmente, pseudo escalarmente y vectorialmente.

Profundicemos un poco más en estas definiciones:

Escalarmente

Sí la trayectoria es conocida y está coordenada de modo que el origen 0 se toma en un punto extremo de la misma el espacio recorrido por el punto móvil P indicará cuál es su posición. Conforme transcurre el tiempo, screce y por tanto su variación 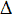s para cualquier intervalo de tiempo será siempre positiva. Esta definición de la posición y de sus cambios es puramente escalar, puesto que no informa sobre el sentido del movimiento.

Pseudo escalarmente

Es posible coordenar la trayectoria conocida, fijado el origen 0 en un punto intermedio. En tal caso la coordenada s puede ser negativa, cuando el punto P está a la izquierda de 0, y positiva cuando está a su derecha.

Si el punto móvil P se dirige de izquierda a derecha el valor de la coordenada s aumenta en cualquier caso y por tanto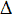 s es positivo. Si el punto P se dirige de derecha a izquierda el sentido del movimiento corresponde al de los valores decrecientes de s, tanto si el móvil está en la parte negativa de la trayectoria como si está en la parte positiva. Ello significa que s es entonces negativo. Por consiguiente el signo de 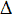s indica, en estos casos, el sentido del movimiento que será de la parte negativa hacia la parte positiva de la trayectoria si 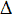s es positivo y opuesto cuando 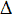s sea negativo.

Vectorialmente

Las coordenadas xe y de un punto P que se mueve en un plano permiten fijar la posición sin necesidad de conocer la trayectoria. Esta forma de definir la posición y sus cambios en un movimiento es la más general y puede expresarse también mediante un segmento orientado o vector, que tenga como origen el origen 0 del sistema de ejes XY y como extremo el punto móvil P. Dicho vector se denomina vector de posición y se representa en la forma r. La línea descrita por el extremo o flecha del vector de posición durante el movimiento es precisamente la trayectoria.

Los cambios o variaciones de la posición se representan en la forma 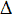r y describen el desplazamiento del móvil en el intervalo de tiempo 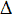t que transcurre entre las posiciones extremas r1 y r2 correspondientes. Este vector 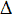r que se denomina vector desplazamiento constituye, por tanto, el vector diferencia de los vectores de posición inicial y final, es decir, 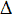r = r2 - r1.

1 2

© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación - www.asocae.org - RNA 592727 - CIF.: G70195805 ¦ Contacto  ¦  Bibliografía ¦  Política de privacidad ¦ Esta web NO utiliza cookies, ni guarda datos personales de los usuarios